Math

主要介绍需要用到的概率论的基础知识以及强化学习中关键术语。

  1. Random Variable

    通常使用大写字母（如：X）表示随机变量, 使用小写字母（如：x, x1）表示随机变量的观测值（observed value），观测值是确定的数，没有随机性。

  2. Probability Density Function（PDF）

    概率密度函数：PDF provides a relative likelihood that the value of the random variable would equal that sample.

    例如：连续的正态分布（也叫做高斯分布）

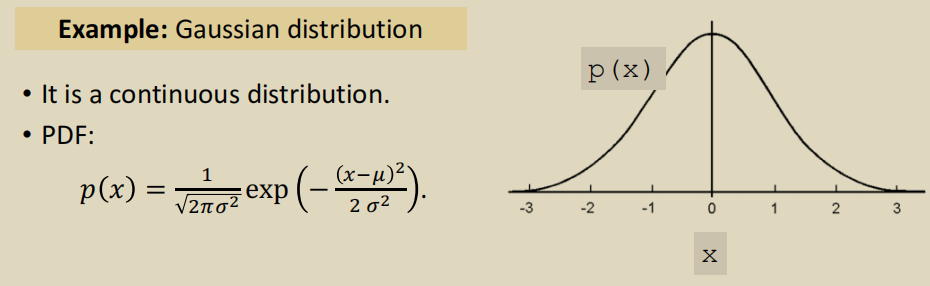
    image-20201214155842957

    离散的分布：

    image-20201214155924736

    假设随机变量 X 的域为 \(\mathbb{X}\)

    1. 连续分布

      \(\int_\mathbb{X} p(x)dx = 1\)

      期望： \(\mathbb{E}[f(x)] = \int_{x\in \mathbb{X}}{p(x) \cdot f(x)}dx\)

    2. 离散分布

      \(\sum_{x \in \mathbb{X}}{p(x)} = 1\)

      期望：\(\mathbb{E}[f(x)] = \sum_{x\in \mathbb{X}}{p(x) \cdot f(x)}\)

  3. Random Sampling

    随机采样：1. 知道各情况种类以及总数，去抽样 2. 知道各情况概率，去抽样。

Terminology

  1. state and action

  2. policy

    Policy function \(\pi\) 是动作 A 的概率密度函数: \(\pi(a|s) = P(A=a|S=s)\) 它是在某状态 s 下，采取某个特定动作（例如：A=a1）的概率。 例如：给定状态 s，动作 A 离散分布的概率密度函数如下：

    • \(\pi(left|s) = 0.2\)
    • \(\pi(right|s) = 0.2\)
    • \(\pi(up|s) = 0.2\)
    • \(\pi(down|s) = 0.2\) 根据选取的策略不同（随机性策略或者确定性策略），从中随机选取或者选取概率最大的 action 进行实施。

  3. reward

  4. state transition

    \(old state \xrightarrow{action} new state\)

    • State transation can be random
    • Randomness is from the environment(状态转移的随机性取决于环境，这里的环境就是游戏程序)
    • 状态转移，用 p 函数表示： \(p(s^{'}|s,a) = \mathbb{P}(s^{'}=s,A=a)\), 如果观察到当前状态 s 和动作 a，P 函数输出状态变为 \(p(s^{'}\) 的概率。

  5. agent environment interaction

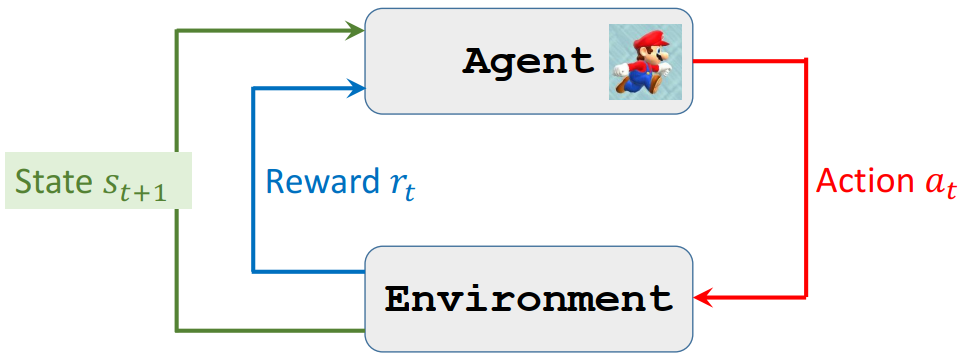
    20201214194035

Randomness in Reinforcement learning

  1. Actions have randomness

    Given state 𝑠, the action can be random

  2. State transitions have randomness

    Given state 𝑆 = 𝑠 and action 𝐴 = 𝑎, the environment randomly generates a new state \(𝑆^{'}\)

Rewards and Returns

Return

Definition: Return (aka cumulative future reward) \(𝑈_{t} = 𝑅_{t} + 𝑅_{t+1} + 𝑅_{t+2} + 𝑅_{t+3} + ⋯\)

  • Future reward is less valuable than present reward.
  • \(R_{t+1}\) should be given less weight than \(𝑅_{t}\)

Discounted return

Definition: Discounted return (aka cumulative discounted future reward)

  • \(\gamma\): discount rate (tuning hyper-parameter)
  • \(𝑈_{t} = 𝑅_{t} + \gamma𝑅*{t+1} + \gamma^2𝑅*{t+2} + \gamma^3𝑅_{t+3} + ⋯\)

At time step 𝑡, the return \(𝑈_{t}\) is random. Two sources of randomness:

  1. Action can be random: \(ℙ[𝐴=𝑎|𝑆=𝑠]=𝜋(𝑎|𝑠)\)
  2. New state can be random: \(ℙ[𝑆^{'}=𝑠^{'}|𝑆=𝑠,𝐴=𝑎]=𝑝(𝑠^{'}|𝑠,𝑎)\)
    • For any 𝑖 ≥ 𝑡, the reward 𝑅n depends on 𝑆n and 𝐴n.
    • Thus, given 𝑠, the return 𝑈 depends on the random variables:
    • \(𝐴_{t},𝐴_{t+1},𝐴_{t+2},⋯\) and \(𝑆_{t+1},𝑆_{t+2},⋯\)

Action-Value Function 𝑄(s,a)

Definition: Action-value function for policy 𝜋

\(𝑄_{\pi}(𝑠_{t},𝑎_{t}) = \mathbb{E}[𝑈_{t}|𝑆_{t}=𝑠_{t}, 𝐴_{t}=𝑎_{t}]\)

  • Return \(𝑈_{t}\) depends on states \(𝑆_{t},𝑆_{t+1},S_{t+2},⋯\) and actions \(A_{t},A_{t+1},A_{t+2},⋯\)
  • 将随机变量 \(𝑈_{t}\) 当作未来所有状态 S 以及未来所有动作 A 的一个函数求期望，将这些变量积分积掉，得到一个数 \(𝑄_{\pi}\)。
  • \(𝑆_{t}, A_{t}\) 被作为观测到的数值而对待，没有被积掉了。因此 \(𝑄_{\pi}\) 的值与 \(𝑆_{t}, A_{t}\) 有关。
  • 积分的时候会用到 Policy 函数，如果 Policy 函数 \(\pi\) 不一样，积分得到的函数 \(𝑄_{\pi}\) 就不一样。

未来状态和动作都有随机性

  • Actions are random: \(\mathbb{P}[A=a|S=s]=\pi(a|s)\), 动作 A 的概率密度函数是 Policy function \(\pi\)
  • States are random: \(\mathbb{P}[S^{'}=s^{'}|A=a]=p(s^{'}|s,a)\), 状态 S 的概率密度函数是 state transition function p.

\(𝑄_{\pi}\) 的意义：采取策略 \(\pi\)，在 \(S_{t}\) 状态下，动作 \(A_{t}\) 的好坏。

Optimal action-value function

用不同的策略 \(\pi\)， 就有不同的 \(𝑄_{\pi}\)， 那如何将 Action-Value function 中的 \(\pi\) 去掉呢？答案是： \(𝑄_{\pi}\) 关于 \(\pi\) 求最大化。

Definition: Optimal action-value function.

\(Q^{\star}\left(s_{t}, a_{t}\right)=\underset{\pi}{\max} Q_{\pi}\left(s_{t}, a_{t}\right)\)

使用最好的策略 \(\pi\)（也就是使得 \(𝑄_{\pi}\) 函数最大化的那个 \(\pi\)），因此 \(Q^{\star}\) 与 \(\pi\) 无关了，它只与 \(S_{t}, A_{t}\) 有关。

\(Q^{\star}\) 的意义：在某个状态 s 下，对动作 a 做评价。

State-value function

  • \(V_{\pi}(s_{t}) = \mathbb{E_{A}}[Q_{\pi}(s_{t}, A)] = \sum{\pi(a|s_{t})\cdot Q_{\pi}(s_{t},a)}\) (Actions are discrete)
  • \(V_{\pi}(s_{t}) = \mathbb{E_{A}}[Q_{\pi}(s_{t}, A)] = \int{\pi(a|s_{t})\cdot Q_{\pi}(s_{t},a)}da\) (Actions are continuous)

将动作 A 当作随机变量，对其进行积分求期望， 其中 A 的概率密度函数 \(A~\pi(\cdot|s_{t})\)，将 A 消掉，然后 \(V_{\pi}\) 函数就只与 \(\pi\) 和 S 有关。

意义：\(V_{\pi}\) 可以告诉我们当前的局势状况好坏优劣。

Value Functions

  1. Action-value function

    \(𝑄_{\pi}(𝑠_{t},𝑎_{t}) = \mathbb{E}[𝑈_{t}|𝑆_{t}=𝑠_{t}, 𝐴_{t}=𝑎_{t}]\)

    For policy \(\pi\), \(𝑄_{\pi}(𝑠_{t},𝑎_{t})\) evaluates how good it is for an agent to pick action a while being in state s.

  2. State value function

    \(V_{\pi}(s*{t}) = \mathbb{E_{A}}[Q_{\pi}(s_{t}, A)] = \sum_{a} \pi\left(a \mid s_{t}\right) \cdot Q_{\pi}\left(s_{t}, a\right)\)

    如果动作 A 的概率密度函数 \(\pi\) 是离散的,则 \(V_{\pi}\) 可以进一步写成求和的形式；如果是连续的，则可写为积分形式。

    For fixed policy \(\pi\), \(V_{\pi}(s_{t})\) evaluates how good the situation is in state s.

    \(\mathbb{E}_{s}[V_{\pi}(S)]\) evaluates how good the policy \(\pi\) is.

Two Methods

  1. Policy-based：Suppose we have a good policy \(\pi(a|s)\).

    • Upon observing the state \(S_{t}\)
    • random sampling \(a_{t}~\pi(\cdot|s_{t})\)

  2. Value-based：Suppose we know the optimal action-value function \(Q^{\star}(s|a)\)

    • Upon observe the state \(S_{t}\)
    • choose the action that maximizes the value \(a_{t} = argmax_{a}Q^{\star}(s_{t},a)\)

几种分类

通过价值选行为 直接选行为 想象环境并从中学习
Q learing Policy Gradient Model based Rl
Sarsa
Deep Q Network

理解环境

根据理解环境与否， 分为 Model-Free RL 与 Model-Based RL

  1. Model-Free

    特点：不尝试理解环境，根据环境的反馈一步步学习 代表：Q Learning、Sarsa、Policy Gradients

  2. Mode-Based

    特点：建模，可以自己训练

概率与价值

基于概率(Policy-Based RL)、基于价值(Value-Based RL)

  1. 基于概率(Policy-Based RL)

    根据所处的环境，判断下一步行动的概率，每一种动作都有可能被选中，只是可能性大小不同 使用连续的概率分布处理选择连续的动作 代表：Policy Gradients

  2. 基于价值(Value-Based RL)

    直接选择价值最高的动作；无法处理连续的动作 代表：Q Learning、Sarsa

  3. 结合 Policy 和 Value 的 Actor-Critic

    Actor： 基于概率做出动作 Critic： 根据做出的动作给出价值

更新频率

  1. 回合更新(Monte-Carlo update) 等待每次训练结束，进行更新 代表：基础版 Policy Gradients、Monte-Carlo Learing

  2. 单步更新(Temporal-Difference update) 训练过程中的每一步都进行更新 代表：Q Learning、Sarsa、升级版 Policy Gradients

在线与离线

  1. 在线学习 本人在场，边玩边学习 代表：Sarsa、Sarsa(Lambda)

  2. 离线学习 可以从他人的经历中进行学习 也可以白天存储学习经验，晚上离线学习 代表：Q Learning、Deep Q Network

Going to learn

  1. Value-based learning.

    • Deep Q network (DQN) for approximating \(𝑄^{\star}(𝑠|𝑎)\).
    • Learn the network parameters using temporal different(TD).

  2. Policy-based learning.

    • Policy network for approximating 𝜋(𝑎|𝑠).
    • Learn the network parameters using policy gradient.

  3. Actor-critic method. (Policy network + value network.)

  4. Example: AlphaGo

资料

  1. 2015 年 David Silver 的经典课程Teaching
  2. 2017 年加州大学伯克利分校 Levine, Finn, Schulman 的课程 CS 294 Deep Reinforcement Learning, Spring 2017
  3. 卡内基梅隆大学的 2017 春季课程Deep RL and Control。