简介

求解线性回归模型函数求极值 解析解 根据严格的推导和计算得到，是方程的精确解能够在任意精度下满足方程 数值解 通过某种近似计算得到的解 能够在给定的精度下满足方程 常用的求数值解的方法：梯度下降法

一元凸函数求极值 对于迭代法来说：

  1. 步长过小，迭代次数过多，收敛慢
  2. 步长过大，产生震荡 overshoot the minimum（更新 x 时，步长太大，跨越了最小值） 震荡：1. 来回震荡，振幅越来越小，最终收敛 2. 来回震荡，无法收敛

让步长和斜率之间保持正比例关系, \(\eta\) 是一个常数，称为学习率 \(step = \eta\frac{df(x)}{dx}\)

超参数：在开始学习之前设置，不是通过训练得到的，学习率就是一个超参数。

选择一组好的超参数，可以提高学习的性能和效果。

第 k+1 轮迭代和第 k 轮迭代的关系式：\(x^{(k+1)}=x^{(k)}-\eta \frac{df(x)}{dx}\)

优点：

  1. 自动调节步长
  2. 自动确定下一次更新的方向
  3. 保证收敛性

16154310451785 梯度

  1. 模为方向导数的最大值
  2. 方向为取得最大方向导数的方向

只要能够把损失函数描述成凸函数，那么就一定可以采用梯度下降法，以最快的速度更新权值向量 w，找到使损失函数达到最小值点的位置。

一元线性回归

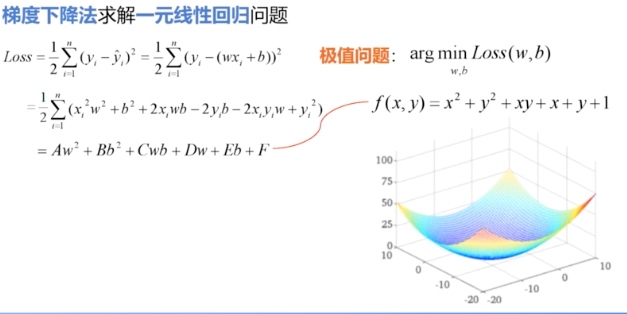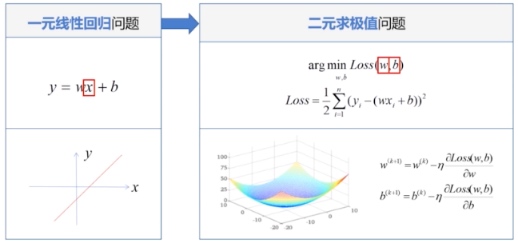
16154312967312 首先，判断一元线性回归的 Loss 为凸函数，然后采用梯度下降法。 16154314178291

16154323224457

步骤：

  1. 加载样本数据 x，y
  2. 设置超参数：学习率，迭代次数 根据经验反复尝试，同时观察算法是否收敛，并达到我们的要求。
  3. 设置模型参数初值 Wo，bo
  4. 训练模型 w，b
  5. 结果可视化
1
2
3
4
5
# 设置超参数
learn_rate = 0.00001  # 通常是一个很小的常数
iter = 100  # 迭代次数

display_step = 10  # 输出结果的间隔，它不属于超参数，因为其取值完全不影响模型训练,只是改变显示的效果

在线性回归中,初始值的选择并没有那么重要,通常情况下我们将其设置为 0 即可.

多元线性回归

归一化/标准化

归一化/标准化：将数据的值限制在一定的范围之内 使所有属性处于同一个范围、同一个数量级下更快收敛到最优解 提高学习器的精度 分为：线性归一化，标准差归一化，非线性映射归一化

  1. 线性归一化：对原始数据的线性变换 \(x^{*}= \frac{x-min}{max-min}\) 等比例缩放 所有的数据都被映射到[0，1]之间
  2. 标准差归一化：将数据集归一化为均值为 0，方差为 1 的标准正态分布 \(x^*= \frac{x一\mu}{\sigma}\)
  3. 非线性映射归一化：对原始数据的非线性变换 指数、对数、正切

使用梯度下降法求解多元线性回归

  1. 加载样本数据 area，room，price
  2. 数据处理 归一化，X，Y
  3. 设置超参数：学习率，迭代次数
  4. 设置模型参数初值 Wo(wo，w1，w2)
  5. 训练模型 W \(W^{k+1} = W^{k}-\eta X^{T}(XW-Y)\) \[ \begin{aligned} \frac{\partial \text { Loss }}{\partial W} &=X^{T}(X W-Y) \\ W^{(k+1)} &=W^{(k)}-\eta \frac{\partial \operatorname{Loss}(W)}{\partial W} \end{aligned} \]
  6. 结果可视化 16154428462423