神经网络

神经网络：人脑智慧的物质基础 神经元/神经细胞：生物神经系统的基本单元

M-P 神经元模型 -1943 年

m-p

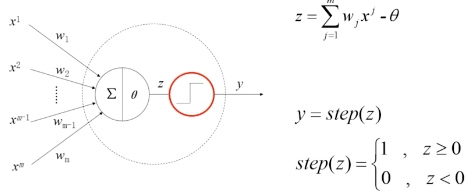
输入信号用来模拟神经元的树突，这些信号的来源不同，影响不同，因此为他们分配不同的权重。

计算单元模拟细胞核，将接收到的输入信号加权求和之后，与产生兴奋的中间结果相比较得到中间结果 z。

最后，通过阶跃函数模拟神经兴奋。阶跃函数被称为激活函数/激励函数(activation functions)

16154641566100

权值向量 W 无法自动学习和更新,不具备学习的能力

感知机模型 - 1957 年 感知机模型分为两层，输入层接受外界信号，输出层为 M-P 神经元，忽略 MP 神经元的细节，可以简化为右下图形式。

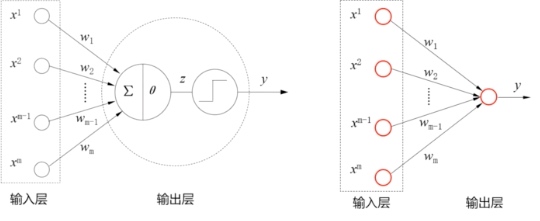输入层不发生计算，因此不计入神经网络的层数，只有输出层是发生计算的功能神经元，因此感知机是单层神经网络。

感知机训练法则：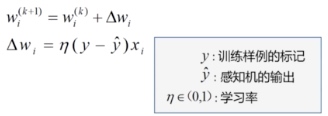

自动调整权值，具备学习能力 第一个用算法来精确定义的神经网络模型 线性二分类的分类器 感知机算法存在多个解，收到权值向量初始值，错误样本顺序的影响。 对于非线性可分的数据集，感知机训练法，则无法收敛

Delta 法则 使用梯度下降法，找到能够最佳拟合训练样本集的权向量。

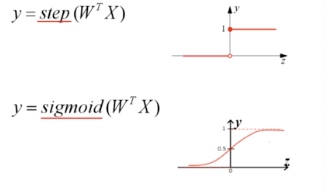
因为阶跃函数具有不连续，不光滑等不太好的性质，实际中，经常使用 sigmod() 函数作为激活函数。 逻辑回归可以看做单层神经网络

多分类问题：设置多个输出节点，在输出层使用 soft max 作为激活函数，得到不同种类的概率。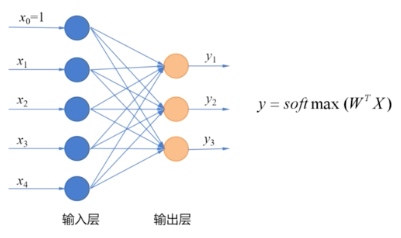

实现单层神经网络

16154682238736

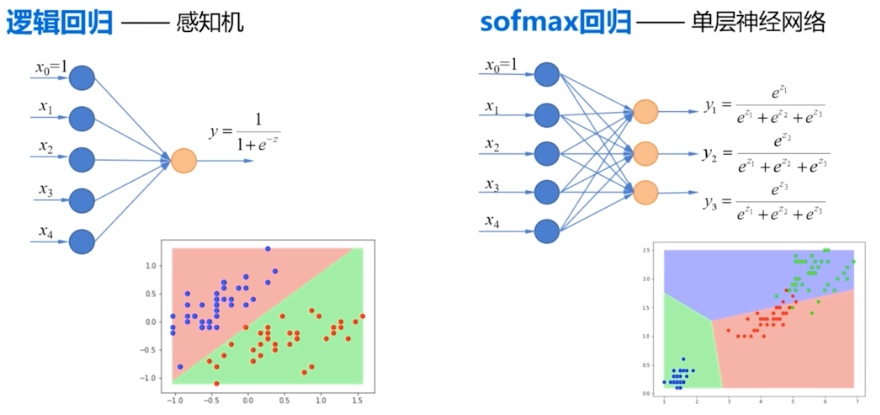
神经网络的设计

1. 神经网络的结构 确定有几层，每层有几个节点，节点之间时如何连接的，使用什么激活函数 单层前馈型神经网络
2. 激活函数 分类问题使用 softmax 函数作为激活函数 标签值使用 one-hot encoding 表示
3. 损失函数 使用交叉熵损失函数来计算误差

神经网络是数学模型，节点与节点之间的关系是数学运算，通过多维数组来实现这些数学运算。

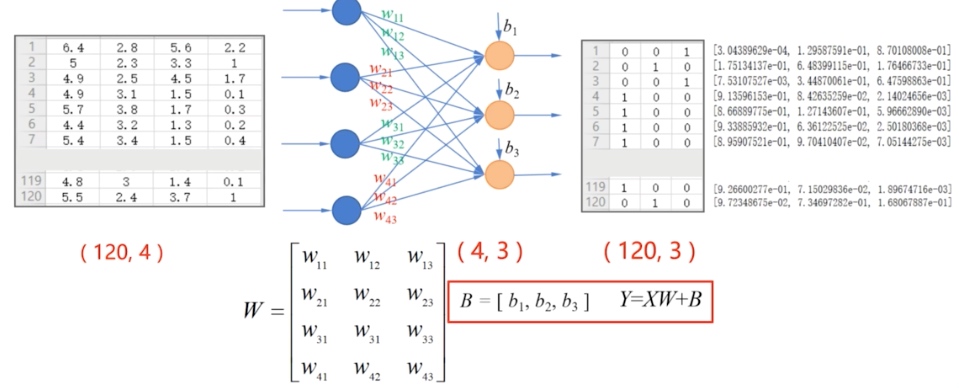
1. softmax 函数 tf.nn.softmax()， tf.nn.softmax(tf.matmul(X-train, W)+b)

2. one-hot encoding tf.one_hot(indices, depth) indices:输入值，要求是一个整数 depth：深度 tf.one_hot(tf.constant(y_test, dtype=tf.int32), 3)

3. 交叉熵损失函数 tf.keras.losses.categorical_croossentropy(y_true, y_pred) y_true: 表示为 one-hot encoding 的标签值 y_pred: 表示为 softmax 函数的输出

4. 平均交叉熵损失 tf.reduce_mean(tf.keras.losses.categorical_crossentropy(y_true = T_train, y_pred=PRED_train)) 也可以使用求和函数得到总的交叉熵损失