polynomial commitment and KZG commitment

Merkle tree commitment:

1. commitment = root hash (For SHA256, 32 bytes)
2. Proof: $log(n)$ proof size
3. Application: state trie / Merkle Patricia Trie

KZG commitment:

1. commitment = 48 bytes (a Jacobian elliptic curve point)
2. Proof: 48 bytes (no matter $n$ is)
3. Multi-point proof/batch proof $y_{i(0)},y_{i(1)},\cdots, y_{i(m-1)}$: 48 bytes (no matter $n$ is)
4. Multi-polynomial commitment、proof aggregation
5. Application: Stateless (Verkle tree), DAS (data availability sampling)

Overall procedures of KZG

1
2
3
4
5

Knowledge ->（Point-Values ->) Coefficients -> Commitment -> Open&Prove&Verify
                          FFT            MSM
                                          ^
                                          |
                                    Trusted Setup

Encode data into Polynomial

Give $(x_i, y_i)$, $x_i \ne x_j \forall i \ne j$, there are two way to encode the data into the polynomial.

1. If the $x_i$ is just indices without other sense, then only data is valuable. The data can be converted into integers and treated as the coefficients of the polynomial.

2. Regardless of whether $x_i$ is a sequential index, whether it stores information or not, these points can be treated as the point-value representation of the polynomials. The Inverse FFT can be used to convert the point-value representation to coefficient representation.

Normally, the binary or integer data are encoded into a finite field $\mathbb{F}_q$, q is a prime such that {0, 1, 2, , q-1} modulo q.

a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. -- wikipedia

Elliptic curve groups are additive groups; that is, their basic function is addition. When it comes to the multiplication of curve points, the pairing is introduced.

Polynomial on Elliptic curve

Elliptic curve $\mathbb{G_1} = [0, G_1, G_1+G_1 = [2]G_2, \cdots, [q]G_1]$, where $[q+1]G_1=0$

$[f(x)]G_1 = [\sum_{i=0}^n a_i x^i]G_1 = \sum_{i=0}^n a_i ([x_iG_1]) = \sum_{i=0}^n a_i [x_i]_1$

Polynomial Commitment with Trusted Setup

a secret $s \in F_q$ can be generates, such that

1. nobody knows the $s$ (private key of 'god')
2. $[s^i]G_1=[s^i]_1, i=1, \cdots$ and $[s^i]G_2=[s^i]_2, j=1, \cdots$ is known to everybody. (public key of 'god')
3. Benefiting from the discrete log problem of the Elliptic curve, no one can recover $s_i$ though $[s^i]_1 or [s^i]_2$

If you are familiar with the secret key in EDCSA signature, that's it. The $[s^i]G_i, [s^i]G_2$ can be seen as the public key.

Nowdays, popular way to generate $s$ is MPC. Besides, Ethereum is doing KZG ceremony, ethereum/kzg-ceremony-specs: Specs for Ethereum's KZG Powers of Tau Ceremony. The degree of $G_2$ is significantly smaller than $G_1$. Therefore, in pairings, the high degree part should match with $G_1$ and the low degree part with $G_2".

Commitment: $Com = [f(s)]_1 = \sum_{i=0}^n [a_i s_i]G_1 = \sum_{i=0}^n a_i [s_i]_1$, where Com is actually a point on the elliptic curve.

From the Schwartz-Zippel Lemma, finding a random $x_0$ such that the probability of $F(x_0) = f(s)$ is impossible.

Single proof

Given $x_i$, we want to prove the computing result $y_i = f(x_i)$,

$$\begin{equation} \begin{aligned} &f(x) - y_i = q(x)(x - x_i) \\ &q(x) = \frac{f(x)-y_0}{x-x_0} \end{aligned} \end{equation}$$

Let's integrate the formula with an elliptic curve,

$$\begin{equation} \begin{aligned} [f(x) - y_i] G_1 &= [q(x)(x - x_i)] G_1 \\ [f(x)]_1 - [y_i]_1 &= ? \end{aligned} \end{equation}$$

However, $q(x) x G_1- q(x) x_i G_1$ cannot be evaluated at coordinate $x=s$ without knowing $s$. To solve the problem, $q(x)$ and $x - x_i$ need to be split into multiplication. While the pairing allows to "multiply" the exponents of two group elements, while the usual group structure only allows adding or subtracting exponents

So let pairing, $e: \mathbb{G_1} \times \mathbb{G_2} \rightarrow \mathbb{G_T}$

$$\begin{equation} \begin{aligned} [f(s) - y_i] G_1 G_2 &= [q(s)(s - x_i)] G_1 G_2 \\ e([f(s) - y_i] G_1, G_2) &= e(q(s)G_1, (s - x_i)G_2) \\ e([f(s)]_1 - [y_i]_1, G_2) &= e([q(s)]_1, [s]_2 - [x_i]_2) \\ e(Com - [y_i]_1, G_2) &= e([q(s)]_1, [s]_2 - [x_i]_2), \end{aligned} \end{equation}$$

where $q(s)_1$ is the proof (48 bytes as a point on an elliptic curve).

Great, the above all can be calculated without $s$.

Note: Not all curve can do pairing, G1 and G2 is pairing-friendly.

For multi-proof, assume that you have an interpolation polynomial I(X) such that $I(x_i) = y_i$, where $(x_i,y_i)$ is a list of evaluation points.

$$q(x) = \frac{f(x)-I(x)}{\prod{(x-x_i)}}$$

Polynomial Commitment 的其他实现

1. KZG：PLONK、Marlin
2. FRI：zkSTARK
3. IPA：Bulletproof
4. IPA + Halo-style aggregation：Halo 2

polynomial commitments

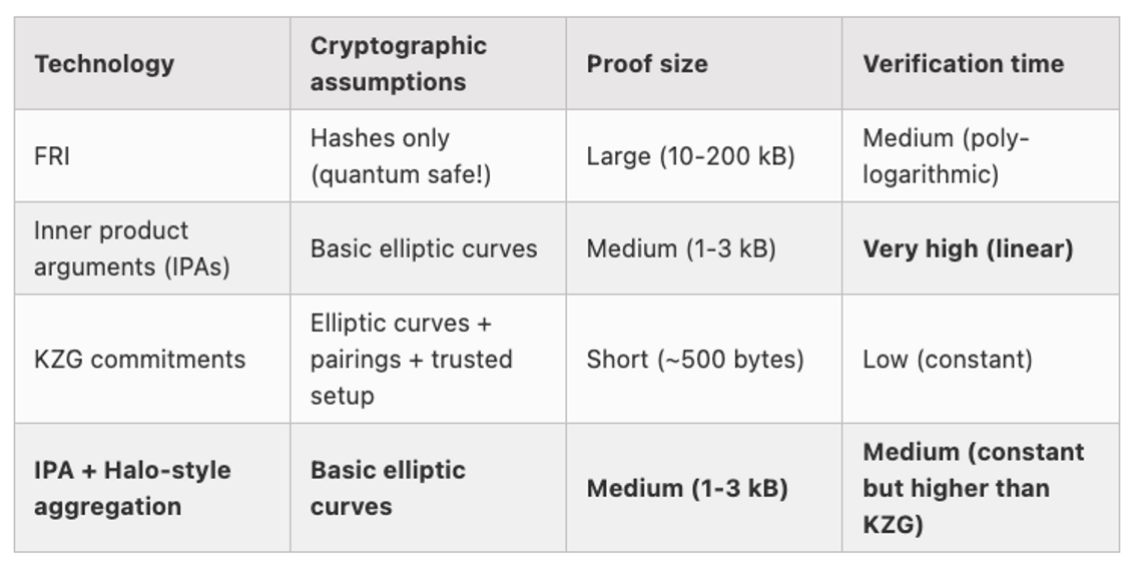
3. KZG Commitment 的优缺点
   1. 缺点：需要 Trusted Setup
   2. 优点：proof 长度短且恒定

TODO

Verkle trees

后面读一下 kzg 原论文

多项式承诺计算就是 MSM，MSM 的高效实现 pippenger 算法

References

1. Recommended KZG 多项式承诺 | Dankrad Feist
2. Polynomial Commitment KZG with Examples ( part 1 ) - YouTube
3. KZG in Practice: Polynomial Commitment Schemes and Their Usage in Scaling Ethereum - Scroll
4. Why "pairings on elliptic curve" are used? - Cryptography Stack Exchange
5. 零知识证明 KZG Commitment 1: Polynomial Commitment 20221129 - YouTube
6. Polynomial (KZG or Kate) Commitment (DappLearning) Notes
7. KZG Polynomial Commitments. This article is based on Dankrad… | by Ozgun Ozerk | Subspace Network
8. [./media/kzg_exercise_sol.pdf]