5. ECC 椭圆曲线

简介

椭圆曲线属于代数几何范畴（algebraic geometry），目前被数论和群论广泛研究，并应用于密码学中。该曲线是一个包含如下形式点的平面代数曲线： \(y^2=x^3+ax+b\)，其中 a 和 b 是常数。不同的参数 a 和 b 会导致不同形状的椭圆曲线。

椭圆曲线的一个重要性质是它们的点可以进行 "加法"运算。通过对两个点进行特殊的加法运算，可以得到一条仍位于该曲线上的新点。这种加法运算的定义是特定的，并且有一些规则。

椭圆曲线在密码学中的应用很多，其中最著名的是用于公钥密码学中的椭圆曲线加密（ECC）。在 ECC 中，椭圆曲线的某个点 G 被用作公开的公钥，而 "加法" 运算过程用于生成互相共享交换的 key，从而实现加密和解密。由于 ECC 需要比其他加密算法使用更短的密钥长度，因此它通常被认为是一种更加安全和高效的加密方法。

运算

定义椭圆曲线上的加法运算：将两个点相加得到第三个点的操作。计算 A+B，过 A，B 两点做一条直线穿过椭圆曲线，然后做关于 x 轴的轴对称：

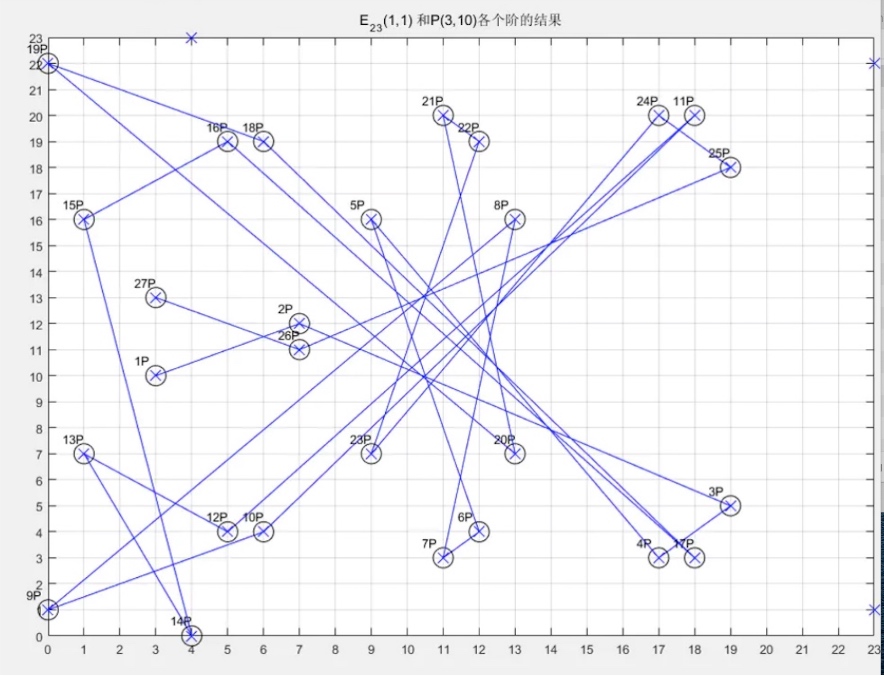
直观感受：观察上图,可以发现虽然点位于曲线上，但相对于整个平面而言，1P 2P 3P 等的位置非常混乱没有规律, 这就是困难问题所在，导致其私钥 k 极其难求。

离散化 -> 有限域

椭圆曲线是连续的，定义在实数域上，并不适合加密。将椭圆曲线变成离散的点，把椭圆曲线映射到一个有限域上，这个过程称：椭圆曲线的离散化或者在有限域上的定义。

为什么要离散化？

为什么连续函数不适合加密，因为实数是连续的，知道结果可以用逆运算求解，函数值随着自变量的变化而连续变化，这意味着在输入值的微小变化下，函数值也会随之微笑地变化，这种连续性使得函数的变化可以攻击者通过输入输出对（明文-密文对）的分析所探测到，这种攻击技术成为“差分分析”。相比之下，离散函数在输入值发生微小变化时，输出值也会发生较大的变化，这使得差分攻击更加困难，因此离散函数更适合加密算法，常见离散函数加密算法包括 RSA，椭圆曲线密码学等。计算机对浮点数的处理会损失精度,产生某些位的浮点位错误，对计算连续函数不友好。举例 1.2-1.0=0.19999999999999996， 7/3=2.3333333333333335

将其映射到有限域上，方便进行离散化的操作，在有限域上就不存在丢失精度问题了。

有限域上的椭圆曲线

有限域上的椭圆曲线上的点数量是有限的。其数量等于有限域的大小 p。该数量包括一个特殊的“无穷远点” （Infinity Point）。
在有限域上，由于点的数量是有限的，所以我们定义椭圆曲线上的倍乘运算，即将一个点诚意一个整数 k，得到另一个点。这个运算可以通过重复进行加法来实现，即将一个点不断地加上自己，直到加了 k 次即得 kG。
符合交换律，结合律，分配律

P+Q 运算：

\(x_3 \equiv k^2 - x_1 - x_2 \mod p\)

\(y_3 \equiv k(x_1-x_3)-y_2 \mod p\)

若 \(P = Q\)，则 \(k = (3x_1^2+a)/2y_1 \mod p\) 若 \(P \ne Q\), 则 \(k = y_2-y_1/(x_2-x_1) \mod p\)

标量乘法 kP, 先做倍数，再做加法（该方法称为：double and add）：

\[ \begin{aligned} 151 & =10010111 \\ & =1 \cdot 2^7+0 \cdot 2^6+0 \cdot 2^5+1 \cdot 2^4+0 \cdot 2^3+1 \cdot 2^2+1 \cdot 2^1+1 \cdot 2^0 \\ & =2^7+2^4+2^2+2^1+2^0+ \\ \text { 即 } 151 P & =2^7 P+2^4 P+2^2 P+2^1 P+2^0 P \end{aligned} \]

ECDLP 椭圆曲线的离散对数困难问题

首先, 任何加密算法可以实现加密的原因都是因为存在一个难解的困难问题, 这个问题的困难程度决定了这个算法的加密强度。

对于 ECC 椭圆曲线上的两个点 P 和 Q，任意整数 k: Q = kP

为什么是困难问题：

给定 k 与 P，根据加法法则，计算 Q 很容易（对应验证过程）

计算过程大致为：将 k 分解为二进制，对应为 2^iP 的加和形式，然后只需要计算极少部分，就可以得到 kP。例如上述例子 151P，只需要计算 P+P，2P+2P，4P+4P，4P+2P, P 并加起来，大概 8 次运算，基本上是枚举次数的 O(logn)。
给定 Q 与 P，求 k 非常困难（在 ECC 的实际应用中，质数 k 取的非常大，想穷举出 k 非常困难）对于攻击者而言，它不知道 k 值，因此需要逐个枚举，151P 则需要计算 150 次。当我们使用椭圆曲线时，选取的 k 非常大。例如假设宇宙中的原子数目为 10^82（大约 2^275），正向计算 Q=kP 的运算量仅仅为 275 个 double-and-add 步骤，而攻击者想要推测 k，则需要 10^82-1 次计算。

所以 Q = kP(k 为大数)，已知 k，P 计算 Q 对我们来说很容易，对攻击者来说，已知 Q P，计算 k 则是困难的。

应用

DH 密钥交换，RSA 算法

5. ECC 椭圆曲线

5. ECC 椭圆曲线

5. ECC 椭圆曲线

简介

运算

离散化 -> 有限域

有限域上的椭圆曲线

ECDLP 椭圆曲线的离散对数困难问题

应用

推荐与参考